2019年北京中考数学难不难?难不难对于每一个人来说答案都是不一样的，所以各位考生问这个问题其实没有多大意义的。并且在招生的过程中都会考虑到试卷难度的这个问题，如果试题过难的话那么很多今年的分数线肯定会有小幅度的下降的，所以各位考生不用过度担心。为了让各位考生对这次考试的难度有一个更清楚的了解，今天小编就来给大家整理了一份关于数学试卷的分析，供各位考生参考。

　　整体分析：

　　试卷100分，要求考生在120分钟内完成。数学试卷包含三个类型的题目：选择题、填空题和解答题，一共有28道小题，从题量上看，题量略大。与别的省市相比，在填空题和解答题的题量上略多，对考生的答题速度有的要求和挑战。

　　其中选择题包含8道小题，每题2分，共计16分;填空题包含8道小题，每题2分，共计16分;解答题有12小题，合计分值68分，相比较别的省份，单题的分值略低，总分值也低一些。

　　除过题量比较大，本张试卷的文字也相对较多，对学生的阅读理解的速度和能力也都有的要去，像选择题的第5题和第8题，填空题第16题，解答题题中的第21,23,24,28题题干都比较长，包含着众多的信息，对学生的读题、分析和理解能力都有比较高的要求。很多学生在做数学题中一见到题干比较长的题时，就会下意识地认为题目难度较大，还没开始解题就已经打退堂鼓了。题干比较长的题目确实有的难度，对学生的理解、分析、总结、观察能力都有比较高的要求，需要学生在短时间内从众多错综复杂的信息中提炼出关键的信心，这对很多阅读理解能力不强的学生来说就是一个很大的挑战，有的同学惊呼，这哪是考数学撒，简直是数学和语文的综合卷，还真的有那么一点意思，学科之间交叉考查已经成为一种命题趋势。

　　整体来看，试卷难度系数适中，没有偏难偏怪的考点和题目，试卷在加强基础知识考查的基础上，还加强了对学生综合能力的考察，尤其是阅读理解能力和灵活运用知识点解决问题的能力。考题比较新颖， 注重知识的拓展和灵活运用，题目的题量和阅读量较大，相对平时的练习题及往年的题目灵活了很多，所以对很多基础一般的学生来说，题目是很有难度的，甚至是难度陡增。

　　选择题分析:

　　第1小题主要考查科学计数法表示比较大的数，比较简单，属于基础题。

　　第2小题主要考查轴对称图形的判断，需要掌握轴对称图形的特征，比较简单，属于基础题。

　　第3小题主要考查正多边形的外角和，需要掌握正多边形的内外角和定理，比较简单，属于基础题。

　　第4小题主要考查数轴，结合动点和相等线段来考查，考查到数形结合思想，综合性相对前几道强了一些，难度有的增加，属于中等题。

　　第5小题主要考查几何与尺规作图结合，难度不大，但题干较长，需要学生具备很强的理解能力，结合题目做出完整的图形再结合几何的相关性质去判断和选择，属于中等题。

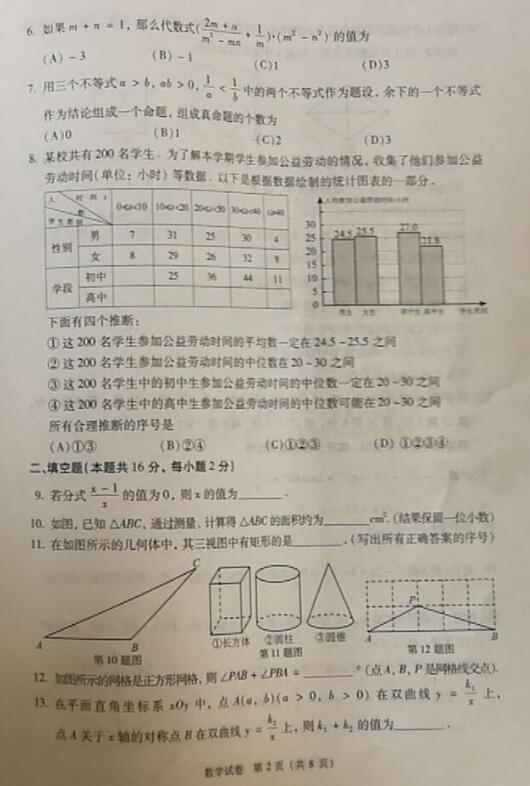
　　第6小题主要考查分式化简求值，主要考查基础的运算能力，先化简，再整体代入求值即可，难度不大，但计算量相对大一些，在计算中需要细心和耐心，属于中等题。

　　第7小题主要考查命题，在解题中需要运用到分类讨论思想，先根据题目要求有序写出三个命题，然后这三个点都可以围绕1/a-1/b展开，结合已知条件去推测其余的条件，再逐一去证明和判断。有难度，比较容易出错。

　　第8小题主要考查数据分析，由于题干中的文字、图表和信息比较多，学生很容易被表格和柱状图中的内容干扰，很难理清头绪，找不到解题的方法，影响解题的状态和速度。这个题目除了考查数学知识和技能外，还考查学生的心理素质和耐心，首先结合题意将表格补充完整，然后结合具体情况进行讨论。题目本身难度不大，但信息错综复杂，比较容易出错。

　　填空题分析：

　　第9小题主要考查分式值为0的条件，比较基础，属于简单题。

　　第10小题主要考查三角形的面积，首先需要去做高，然后测量出一组对应的底和高的数据，然后计算即可，比较基础，属于简单题。

　　第11小题主要考查三视图，掌握常见几何体的三视图是解决本题目的关键，比较简单，属于基础题。

　　第12小题主要考查网格三角形，需要通过做辅助线来解答，还需要运用等面积法求出相关的线段的长度，再结合锐角三角函数计算出相关角的三角函数值，涉及的考点比较多，有的难度。

　　第13小题主要考查反比例函数的图像和性质，可以结合已知条件画出符合条件的草图，然后进行分析和计算，运用到数形结合和代数思想，属于中等题。

　　第14小题主要考查菱形的性质及图形的变化，对学生的观察能力有的要求，虽然看起来比较繁琐和复杂，但只要理解了图二和图三中给定线段的长度的意思，列出简单的方程解方程求出菱形的对角线即可，然后再计算面积，需要结合图形去分析和思考，属于中等题。

　　第15小题主要考查数据分析中的方差，需要理解方差的含义、算法及特征，可以直接计算出两组数据的方差再比较，也可以结合方差和含义和特征来分析，比较基础，属于简单题。

　　第16小题主要考查特殊四边形的判定和性质，综合性较强，需要结合图形去分析和判断，熟练掌握和灵活运用各种特殊四边形的判定和性质时解决本题目的关键，有的难度。

　　解答题分析：

　　第17小题主要考查实数和三角函数的混合运算，基础的计算题，难度不大，但主要注意计算细节，在计算时要细心，比较基础，属于简单题。

　　第18小题主要考查一元一次不等式组的解法，比较简单，掌握一元一次不等式组的解法和解集的求法是解决本题的关键，比较基础，属于简单题。

　　第19小题主要考查特一元二次方程根的判别式及根与方程的解法，首先根据方程有实根得到关于m的不等式，解不等式再结合m为正整数，求出m的值，得到完整的方程解方程即可。

　　第20小题主要考查特菱形的性质和四边形的证明及计算，第1小问可以用比例线段来解答也可以用等腰三角形的性质来证明;第2问需要先将图形补充完整，再证明角相等，然后结合三角函数值进行计算即可。

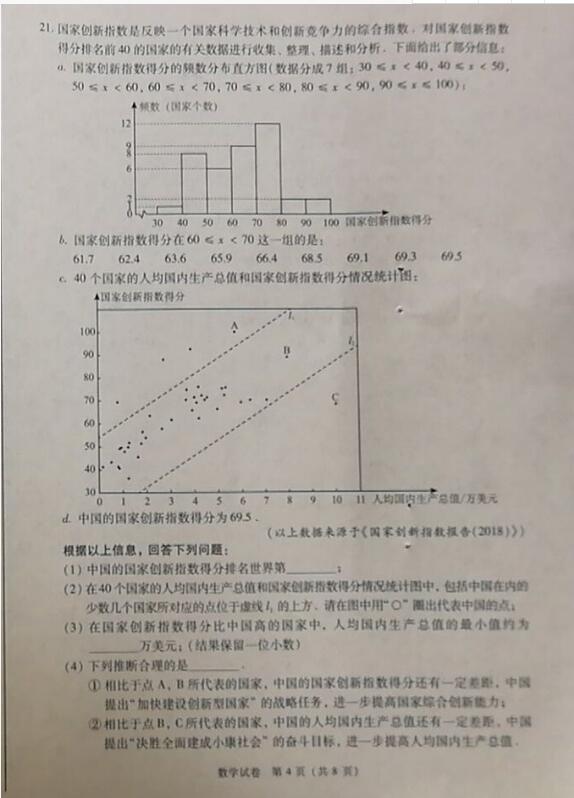
　　第21小题主要考查统计图表的分析，难度不大，但是信息量比较大，读懂题目去分析和计算即可，读懂题目是关键，需要有足够的耐心。

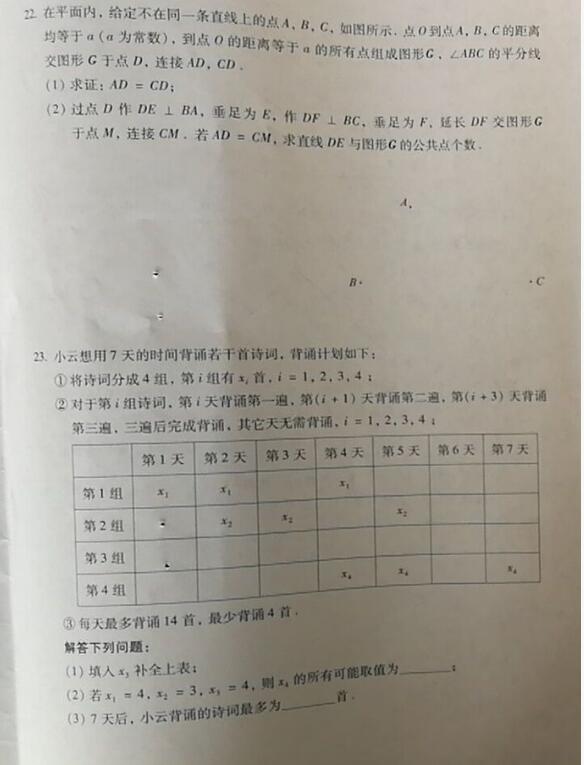
　　第22小题主要考查圆的定义、圆周角与线段的关系、垂径定理等，考查形式新颖，对学生的理解能力和灵活运用能力有比较高的要求。首先要知道在同一个圆中，相等的圆周角所对应的弧长相等，所对应的弦长相等。此外还需要掌握直线与圆相切时，会垂直于过该点的半径，此时直线与圆只有一个焦点。首先根据圆的定义作图，找出对应点再进行分析和证明即可。

　　第23小题主要考查学生的逻辑推理和计算能力，第一问不难，只要根据题意即可表示出来。而第二问列不等式组的关键在于题中告知的单日较多背诵14首，较少背诵4首。第三问相对而言难一些，首先要读懂题中要我们求的是什么。7天背诵的诗词那就是x1+x2+x3+x4，那么接下来的思路和第二问类似，建立不等式组，较终求出x1+x2+x3+x4的取值范围，然后取满足条件的较大整数即可。这儿的难点在于对不等式组的变形合并等。

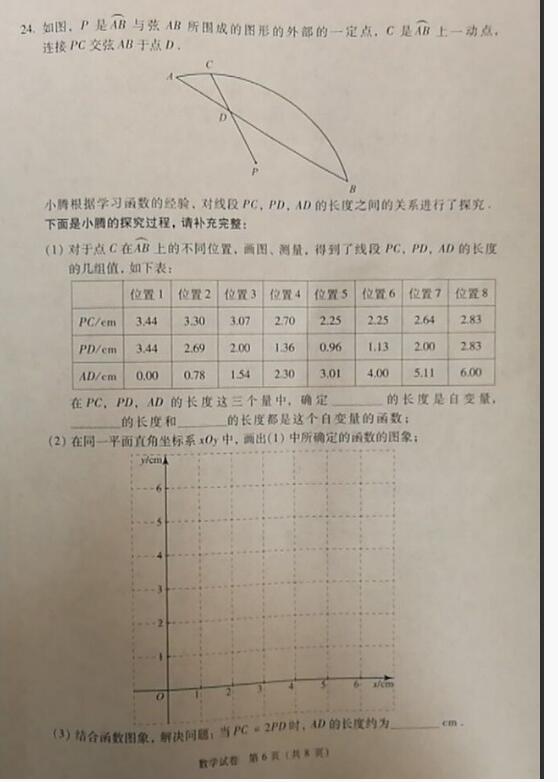
　　第24小题主要考查函数探究，题干看起来很长，但只要理解题意就很简单了。简单的描点绘图，然后直接写结论就行了，送分题，比较基础。

　　第25小题主要考查一次函数的图像和性质，考察到一次函数中的整点问题，有的难度。第一问比较基础，要正确解答第二问，首先要搞清楚整点的定义，然后列出一个不等式组，将范围内的合适的横纵坐标带入不等式检验，找出符合题意的点的个数即可。那么要想没有整点，那么说明边界点之间的距离不能过1，如果过了肯定有整点。如果刚好为1，那么就需要得增加边界点的坐标需要是整数，因为如果不是整数，那说明他们之间肯定有整点。根据这个思路来求解这道题就对了。为了便于分析，要先将各点坐标在图中标示出来，不然很容易乱。

　　第26小题主要考查二次函数的图像和性质，第一问和二问都是比较基础，第三问考查到函数与方程的关系，在二次函数和线段交点确定的条件下，抛物线顶点坐标的变化对于函数图像与线段的交点情况的影响，需要画图结合图像分析，在解题的过程中需要运用到分类讨论思路，要增加抛物线与线段恰有一个公共点，那么Q点需要位于B点上方或者和B点重合，这就是解题的关键所在。

　　第27小题是一道几何综合题，主要考查到三角形与图形换、圆的相关知识点，轴对称的性质、等腰三角形的性质和判定等，题目涉及的知识点比较多，综合性较强，第一问按照要求补充完整图形，难度不大，第二问也是比较简单的证明，就是利用角的关系进行简单变换即可证明结论。第三问的解答中需要利根据题目条件结合动点轨迹做辅助圆来解答，难度较高。还有另外一种思路：要增加ON与PQ恒等，那么就得想办法将他们两个表示出来。那么就得添加辅助线，先证明两个三角形全等，得出边的关系，再利用勾股定理将ON与PQ分别表示出来，得到方程解方程即可。

　　第27小题是一道与圆形相关的新定义类型的题目，首先要理解中内弧的含义的特征，重点在理解题目所定义的点构成的圆弧与三角形各边交点之间的关系。

　　第一问难度不大，在画图之前，我们首先应该去分析在什么情况下中内弧较长?可以先进行简单的画图尝试，经过探索和分析发现当与底边相切时，内弧较长。再根据D/E两点都在圆上，且圆与BC相切，做出符合条件的圆即可。

　　第二问的第一小问，已知t的值，即可确定已知三个点的坐标，并且根据点D/E的特征，求出点D/E的坐标，然后在平面直角坐标系中描出各点，做出简图，求纵坐标的取值范围，只需要找出临界值即可。在这道题目中两个临界点就是与BC边相切以及和AC边相切。分别求出这两种情况下得P点坐标，然后判断出较终的纵坐标取值范围。

　　第二小问，和第一小问有些类似，但有所区别，区别就在于在于此时C点坐标不确定，也就是C点未知，是个动点，那么也就导致了E点也是一个动点，需要根据题意用含有t的代数式表示出E点的坐标，再几何图形去分析。总体思路相同，找出两个临界值，利用三角形相似，求出此时t的值，然后再判断t的取值范围。这道题目作为卷的题，还是比较具有难度的。

　　总的来说，2019年北京中考数学难度不小，题量比较大，综合性比较强，对学生的知识迁移和灵活运用能力有比较高的要求，初中数学中的重难点知识都考查到了，并且考查的方式和角度都比较新颖，对于基础不够扎实，思维和理解能力不强的学生来说，真的是有难度的，不论是题量还是题的深度对考生都是不小的挑战。